Área y volumen de un cilindro

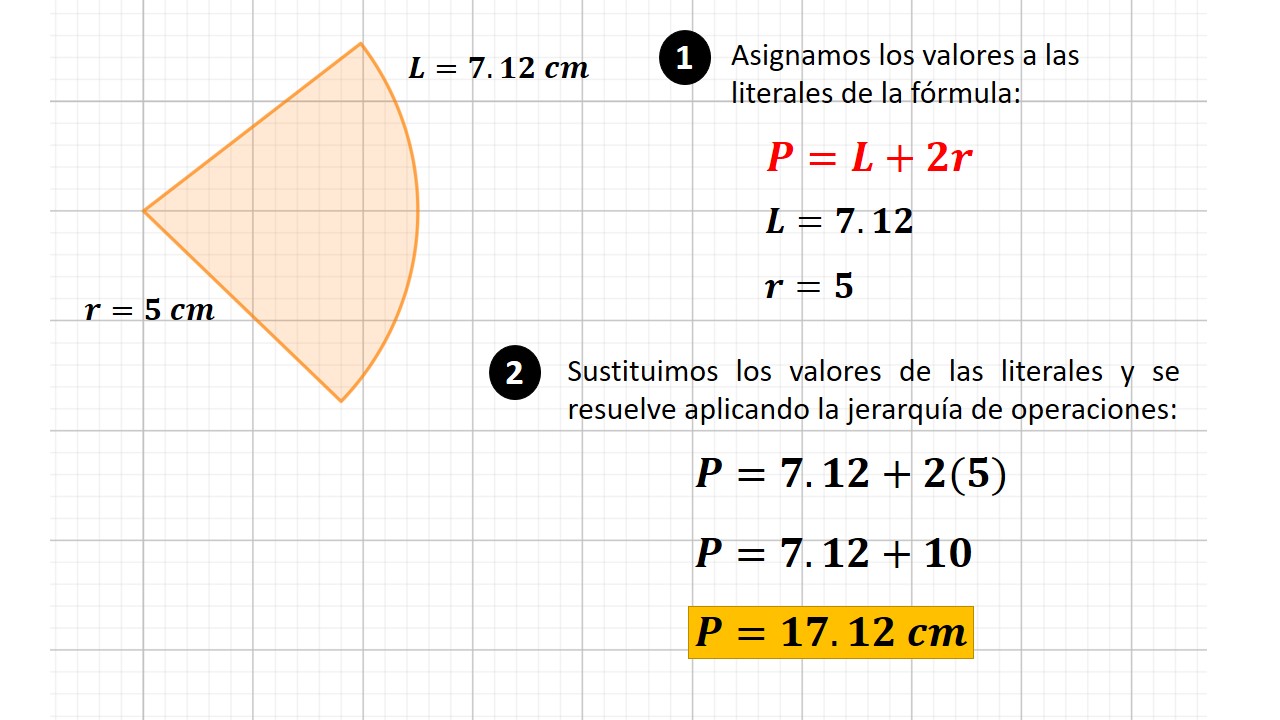
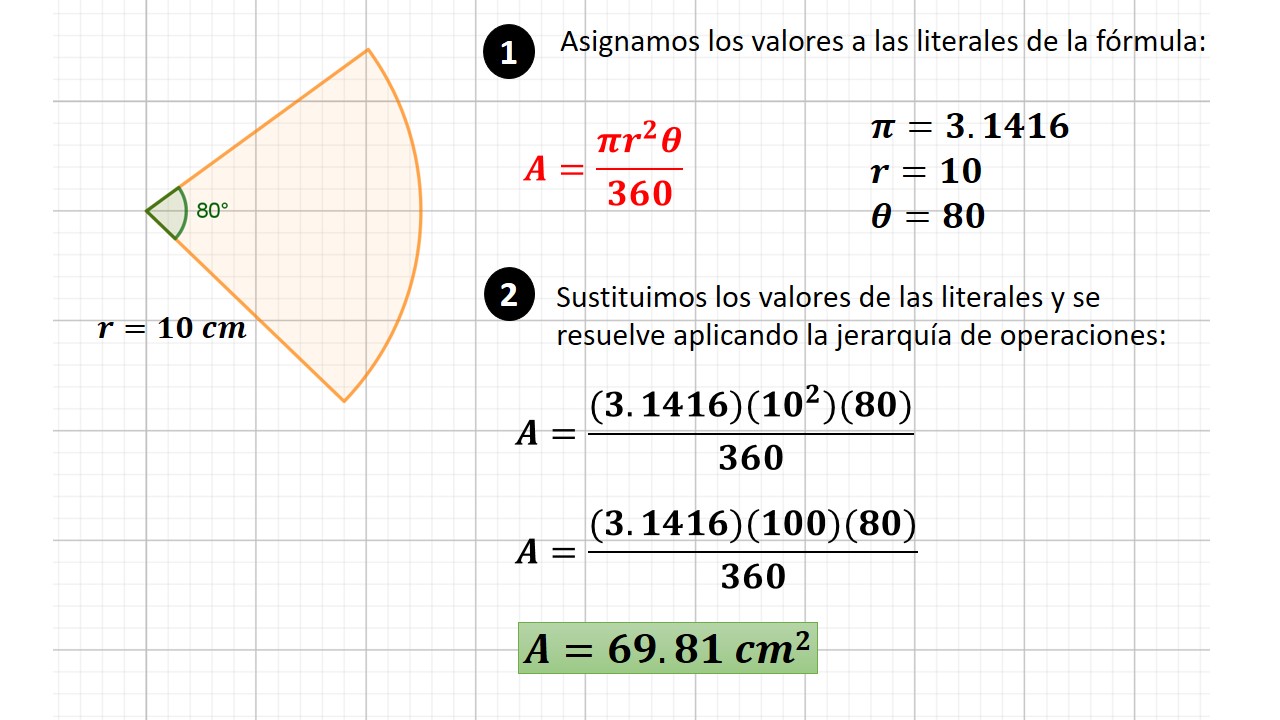
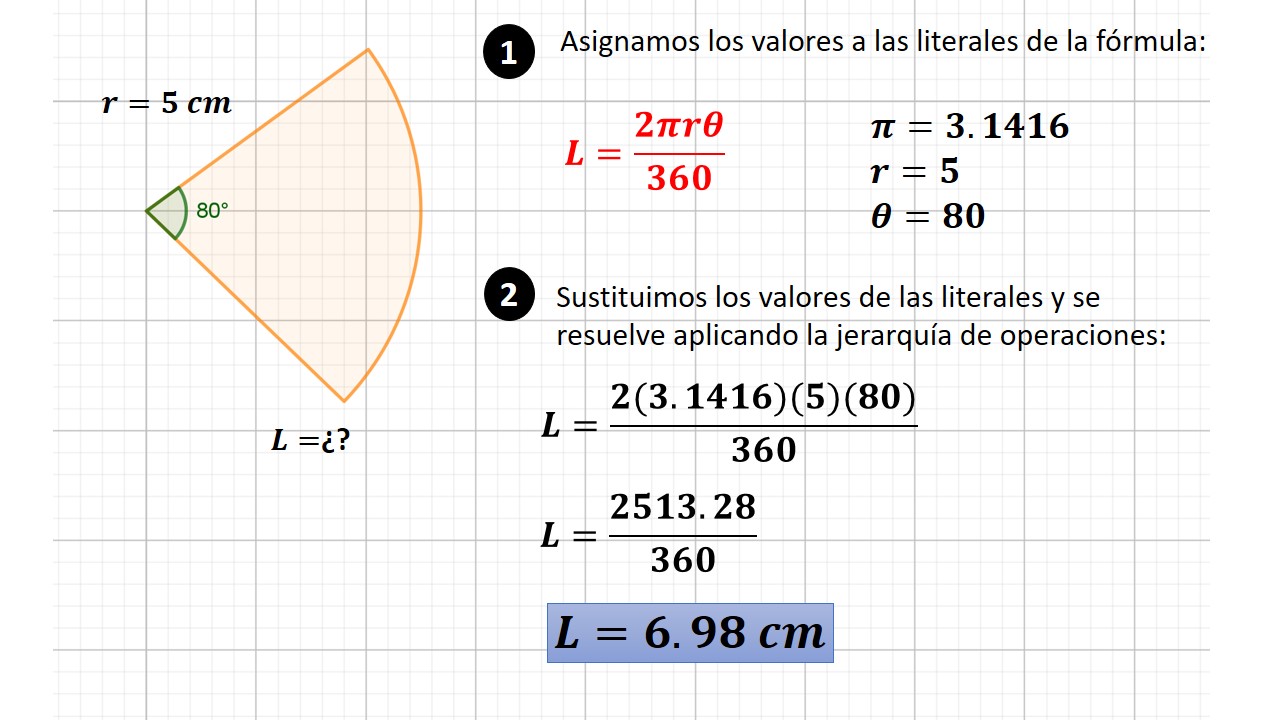
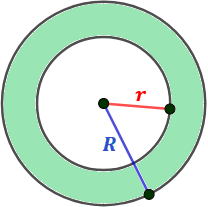
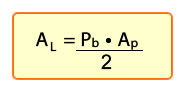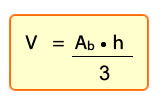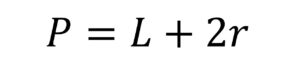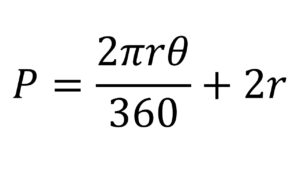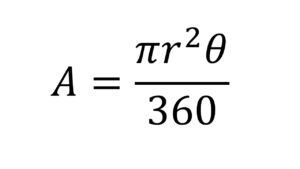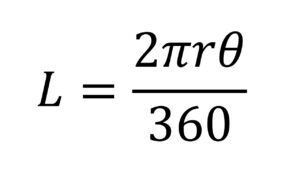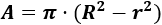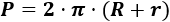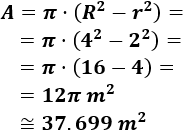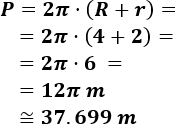¿Qué es un cilindro?

un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz, a lo largo de una curva plana, denominada directriz.

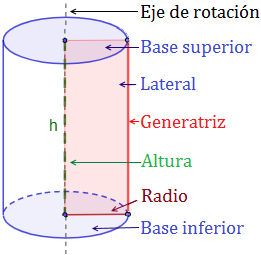
Elementos del cilindro

Área del cilindro

El área del cilindro de radio R y altura h es

Volumen del cilindro

El volumen del cilindro de radio R y altura h es

Ejemplo: 

Calcular el área y el volumen de un cilindro de radio R = 3 cm y altura h = 1 m.

El radio es R = 3 cm.

Como la altura está escrita en metros y el radio en centímetros, tenemos que cambiar una de las unidades.

Pasamos la altura a centímetros:

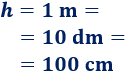
Calculamos el área:

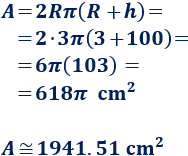
El área es, aproximadamente, 1941.51 cm².

Calculamos el volumen:

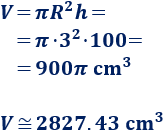
El volumen es, aproximadamente, 2827.43 cm³.

Área y volumen de un prisma

¿Qué es una prisma?

Un prisma, en geometría, es un poliedro que consta de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos. Los prismas se nombran por la forma de su base, por lo que un prisma de base pentagonal se llama prisma pentagonal.

Como vemos, este prisma hexagonal tiene 6 caras laterales que son rectángulos y 2 bases que son hexágonos.

El área lateral de un prisma es la suma de las áreas de sus caras laterales (los 6 rectángulos).

Las 6 caras laterales forman un rectángulo cuya base es el perímetro del hexágono de la base.

Áreas del prisma

Por tanto, el área lateral del prisma es igual al producto del perímetro de la base por la altura:

Área lateral = perímetro de la base x altura

El área total es la suma del área lateral más el área de las 2 bases:

Área total = Área lateral + Área de la base x 2

Volumen del prisma

El volumen del prisma recto, ortoedro, se calcula multiplicando las longitudes de las tres aristas convergentes a un vértice. Es lo que habitualmente llamamos largo, ancho y alto.

Volumen ortoedro = largo x ancho x alto

Por ejemplo, si las aristas de un prisma recto son 12, 5 y 5 cm, entonces

V = 12 cm x 5 cm x 5 cm = 300 cm³

Área y volumen de pirámides

¿Qué es una pirámide?

La pirámide regular es un cuerpo geométrico limitado por un polígono regular, llamado base, y por tantos triángulos como lados tenga la base.

Se nombran diciendo PIRÁMIDE y el nombre del polígono de la base. (Ejemplo: Pirámide cuadrangular, pirámide hexagonal).

Podemos hallar el área lateral, área total y volumen de este cuerpo geométrico, utilizando las siguientes formulas:

1.1- Área lateral

El área lateral es igual al perímetro del polígono de la base multiplicado por la altura de una cara lateral ( AP o apotema) de la pirámide y dividido entre 2.

Pb =perímetro de la base (suma de los lados)

AP = apotema de la pirámide o altura lateral

1.2- Área total

El área total es igual al área lateral más el área del polígonos de la base.

1.3- Volumen

El volumen es igual al área del polígono de la base multiplicado por la altura ( h ) de la pirámide y dividido entre 3.

Donde:

Ab =área basal de la pirámide

h = altura de la pirámide.

EJEMPLO:

1- El área total de una pirámide cuya base es un rectángulo de lados 5cm y 11 cm, y su apotema 8 cm, es igual a:

Pb = perímetro de la base

Pb = suma de los lados

Pb = 11+ 5 + 11 + 5

Pb = 32

Luego debemos calcular el área lateral:

AL = Pb • h / 2

AL = 32 • 8 / 2

AL = 128

Ahora debemos calcular el área de la base:

Ab = base • altura

Ab = 11 • 5

Ab = 55

Ahora que tenemos el área lateral, podemos calcular el área total

AT = AL + Ab

AT = 128 + 55

AT = 183 cm²

Por lo tanto el área total es de 183 cm²

AREA Y PERIMETRO DE UN SECTOR CIRCULAR

¿Qué es un sector circular?

Se denomina sector circular a la porción del círculo determinada por un ángulo central formado por dos radios; Quedando así delimitada por un arco y dos radios.​

Perímetro de un sector circular

El perímetro (P) de un sector circular es la suma de la longitud su arco más dos veces su radio.

Calcular el perímetro conociendo la medida del radio y la longitud del arco.

Para calcular el perímetro de un sector circular donde se conoce: Longitud de la circunferencia (L).

radio.

Se emplea la siguiente fórmula:

Donde:

P = perímetro

L = longitud del arco

r = radio

Ejemplo

Calcular el perímetro conociendo la medida del radio y el ángulo central del sector circular.

Para calcular el perímetro de un sector circular cuando solo se conoce la medida de: radio, ángulo central

Se emplea la siguiente fórmula:

Donde:

P = perímetro

π = 3.14 o 3.1416

r = radio

θ = ángulo central

360 = es la constante de giro que compone una circunferencia.

Ejemplo 

Área de un sector circular

El área de un sector circular es la medida de la superficie plana que está delimitada por un arco y sus dos radios.

Calcular el área de un sector circular conociendo la medida del radio y el ángulo central.

Para realizar este cálculo ocupamos la fórmula:

Donde:

A = área

π = 3.14 o 3.1416

r = radio

θ = ángulo central

Ejemplo 

Longitud del arco

Para calcular la longitud del arco de un sector circular se aplica la siguiente fórmula:

Donde:

L = longitud del arco

π = 3.14 o 3.1416

r = radio

θ = ángulo central

A continuación revisemos los siguientes ejemplos:

Ejemplo 

 

AREA Y PERIMETRO DE UNA CORONA CIRCULAR

¿QUE ES UNA CORONA CIRCULAR?

Una corona circular es la figura geométrica delimitada por dos circunferencias con el mismo centro (concéntricas) y radios distintos (R>r):





En la representación, R es el radio de la circunferencia exterior y r es el radio de la circunferencia interior.


Fórmulas

Las fórmulas del área y del perímetro de una corona circular se obtienen a partir de las fórmulas de la circunferencia. Recordamos que el área delimitada por una circunferencia de radio R es πR2 y su perímetro es 2πR.

Si R es el radio mayor (circunferencia exterior) y r el radio menor (circunferencia interior) de una corona circular, entonces:

El área de la corona circular es

El perímetro de la corona circular es






Ejemplo: Calcular el área y el perímetro de una corona circular delimitada por dos circunferencias con radios 2 y 4 metros.



Solución:


El radio de la circunferencia exterior es R=4m y el radio de la circunferencia interior es r=2m.
Por tanto, el área de la corona circular es







Y el perímetro es

AREA Y PERIMETRO DE UNA CIRCUNFERENCIA

¿QUE ES UNA CIRCUNFERENCIA?

La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.

¿COMO CALCULAR EL PERIMETRO DE LA CIRCUNFERENCIA?

Dada una circunferencia, el perímetro de una circunferencia es la longitud de la curva, es decir, la distancia que caminaría una persona que empezara a caminar en un punto de la circunferencia y diera una vuelta alrededor de la circunferencia hasta llegar al punto de partida.

Se obtiene por medio de la expresión: 

P = 2 x π x r

¿COMO CALCULAR EL AREA DE LA CIRCUNFERENCIA?

La curva denominada circunferencia encierra en su interior una superficie. Esta superficie se llama área de la circunferencia.

Existe una fórmula muy sencilla que nos permite calcular cuál es el área encerrada dentro de la circunferencia sólo sabiendo cuánto mide el radio de la circunferencia.

Llamemos r al radio de la circunferencia, entonces el área de la circunferencia será:

A = π x r²

REFORZANDO CONTENIDO

IDENTIFIQUE LAS PARTES DE UNA CIRCUNFERENCIA

AREA Y PERIMETRO DE UN POLIGONO REGULAR DE n LADOS

¿QUE ES UN POLIGONO REGULAR?

Un polígono regular es aquella figura geométrica que tiene todos sus lados de la misma longitud. A su vez, sus ángulos interiores también comparten la misma medida.

Recordemos que un polígono regular se compone de:

n lados iguales.

n ángulos internos iguales.

PERIMETRO DE UN POLIGONO REGULAR

Perímetro (P): Se multiplica el número de lados (n) por la longitud (L) de cada lado.

Donde:

P = perímetro

n = número de lados

l = longitud del lado

AREA DE UN POLIGONO REGULAR

Área (A): Se multiplica el perímetro (P) por la apotema (a) y se divide entre dos.

Donde:

A = área

P = perímetro

a = apotema

APOTEMA: El apotema de un polígono regular es la distancia que hay del centro del polígono al punto medio de cualquiera de sus lados.

EJEMPLO 1: Calcular el perímetro y área de un pentágono que mide 5 cm por lado y 3.44 cm de apotema.

EJERCICIO 2: Calcular el perímetro y área de un dodecágono que mide 5 cm por lado y 9.18 cm de apotema.

EJERCICIO: Supongamos que tenemos un polígono regular de seis lados donde cada lado mide 12 metros ¿Cuál es el perímetro y área de la figura?